Using GeneticSharp for Optimizing Building Design in the AEC Industry

Introduction
In the AEC industry, building design is an intricate balance of various constraints. From cost and material limitations to structural and environmental factors, creating an optimal design can be a daunting task.
The implementation of Genetic algorithms, called Generative Design, offers a powerful way to explore multiple solutions and find the best fit.
There are some great tools in the market like Autodesk Generative Design, Hypar, Tesfit or even Galapagos in Grasshopper, but what if you want to create your own optimization tool?
In this post, we’ll explore how to use GeneticSharp, a fast and extensible library for implementing genetic algorithms, to solve an optimization problem relevant to the AEC industry.
Specifically, we’ll focus on designing a building that meets constraints like maximum height, total cost and more.
We’ll walk through an example of how to use GeneticSharp to iterate over multiple designs and find the most optimal one.
What is GeneticSharp?
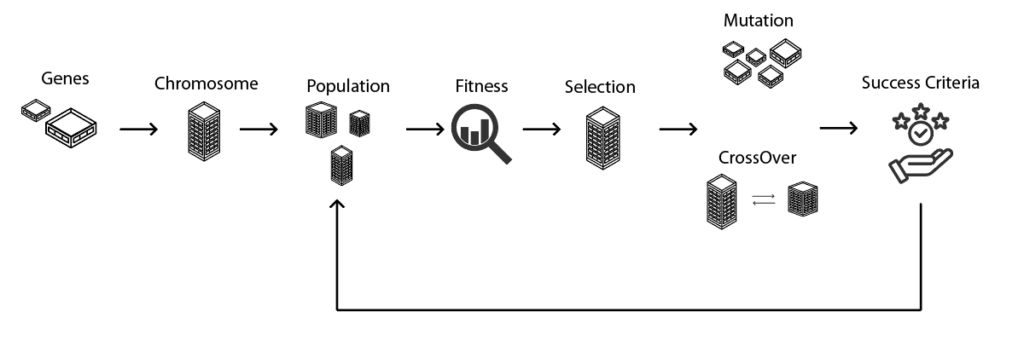
GeneticSharp is a powerful library for running genetic algorithms, mimicking natural selection by evolving solutions through selection, crossover, mutation and replacement.
This technique helps solve complex optimization problems, like finding the best design for a building with competing constraints.
Problem Definition: Optimizing Building Design
Let’s define a simple building design optimization problem. The goal is to design a building that satisfies several constraints:
- Cost constraint: The total cost of materials should not exceed a budget.
- Height constraint: The building must have a height within a specified limit.
- Area constraint: The building footprint must fit within a defined lot area.
We’ll use GeneticSharp to iterate over different combinationsv of floors and materials to find the best design.
Setting Up GeneticSharp
First, install the GeneticSharp library by adding the NuGet package to your project:
Install-Package GeneticSharp
Defining the Building Model
In this example, we simplify the building to be composed of floors, with each floor having a cost, height and a set of base vertices that define its footprint.
public class Floor
{
public double Height { get; set; }
public List<(double x, double y)> BaseVertices { get; set; }
public double Cost { get; set; }
// Method to generate a random floor with base vertices and height
public static Floor GenerateRandomFloor()
{
var random = new Random();
double width = random.NextDouble() * 10 + 5; // Random width between 5 and 15 meters
double depth = random.NextDouble() * 10 + 5; // Random depth between 5 and 15 meters
double height = random.NextDouble() * 4 + 2; // Random height between 2 and 6 meters
var baseVertices = new List<(double x, double y)>
{
(0, 0),
(width, 0),
(width, depth),
(0, depth)
};
double cost = width * depth * height * 100; // Cost function based on volume
return new Floor
{
Height = height,
BaseVertices = baseVertices,
Cost = cost
};
}
}
Next, we define the building as a collection of floors:
public class Building
{
public List<Floor> Floors { get; set; }
public double TotalHeight => Floors.Sum(f => f.Height);
public double TotalCost => Floors.Sum(f => f.Cost);
public Building()
{
Floors = new List<Floor>();
}
}
Defining the Genetic Algorithm
1. Chromosome Definition
A chromosome represents a possible solution to the problem. Each chromosome will represent a building design, with each gene representing a floor.
public class BuildingChromosome : ChromosomeBase
{
public BuildingChromosome(int numberOfFloors) : base(numberOfFloors)
{
for (int i = 0; i < numberOfFloors; i++)
{
ReplaceGene(i, GenerateRandomFloor());
}
}
public override IChromosome CreateNew()
{
return new BuildingChromosome(Length);
}
public override Gene GenerateGene(int geneIndex)
{
return GenerateRandomFloor();
}
private Gene GenerateRandomFloor()
{
return new Gene(Floor.GenerateRandomFloor());
}
}
2. Fitness Function
The fitness function evaluates how well a particular building design satisfies the constraints. We want to maximize the height while minimizing the cost.
public class BuildingFitness : IFitness
{
private readonly double _maxHeight;
private readonly double _maxCost;
public BuildingFitness(double maxHeight, double maxCost)
{
_maxHeight = maxHeight;
_maxCost = maxCost;
}
public double Evaluate(IChromosome chromosome)
{
var buildingChromosome = chromosome as BuildingChromosome;
var building = CreateBuildingFromChromosome(buildingChromosome);
if (building.TotalHeight > _maxHeight || building.TotalCost > _maxCost)
{
return 0; // Invalid solution
}
return (building.TotalHeight / _maxHeight) - (building.TotalCost / _maxCost);
}
private Building CreateBuildingFromChromosome(BuildingChromosome chromosome)
{
var building = new Building();
foreach (var gene in chromosome.GetGenes())
{
building.Floors.Add((Floor)gene.Value);
}
return building;
}
}
3. Genetic Algorithm Execution
We can now set up the genetic algorithm, using the chromosome and fitness function defined above.
var selection = new EliteSelection();
var crossover = new UniformCrossover();
var mutation = new TworsMutation();
var population = new Population(50, 100, new BuildingChromosome(10));
var fitness = new BuildingFitness(60, 100000); // 60 meters max height, $100,000 max cost
var ga = new GeneticAlgorithm(population, fitness, selection, crossover, mutation);
ga.Termination = new FitnessStagnationTermination(100);
ga.Start();
var bestChromosome = ga.BestChromosome as BuildingChromosome;
var bestBuilding = CreateBuildingFromChromosome(bestChromosome);
SaveBuildingToJson(bestBuilding, "C:\\\\Users\\\\User\\\\Desktop\\\\building_design.json");
Validating the Results
To visualize the result, I created a Python node in Dynamo that renders the building’s 3D model:
import json
import clr
from Autodesk.DesignScript.Geometry import Point, PolyCurve, Surface
json_file_path = IN[0] # Input JSON file path
with open(json_file_path, 'r') as json_file:
building_data = json.load(json_file)
floors = building_data['Floors']
dynamo_floors = []
previousHeight = 0
for floor in floors:
vertices = floor['BaseVertices']
height = floor['Height'] + previousHeight
previousHeight = height
points = [Point.ByCoordinates(v['x'], v['y'], height) for v in vertices]
polycurve = PolyCurve.ByPoints(points, True)
surface = Surface.ByPatch(polycurve)
dynamo_floors.append(surface)
OUT = dynamo_floors
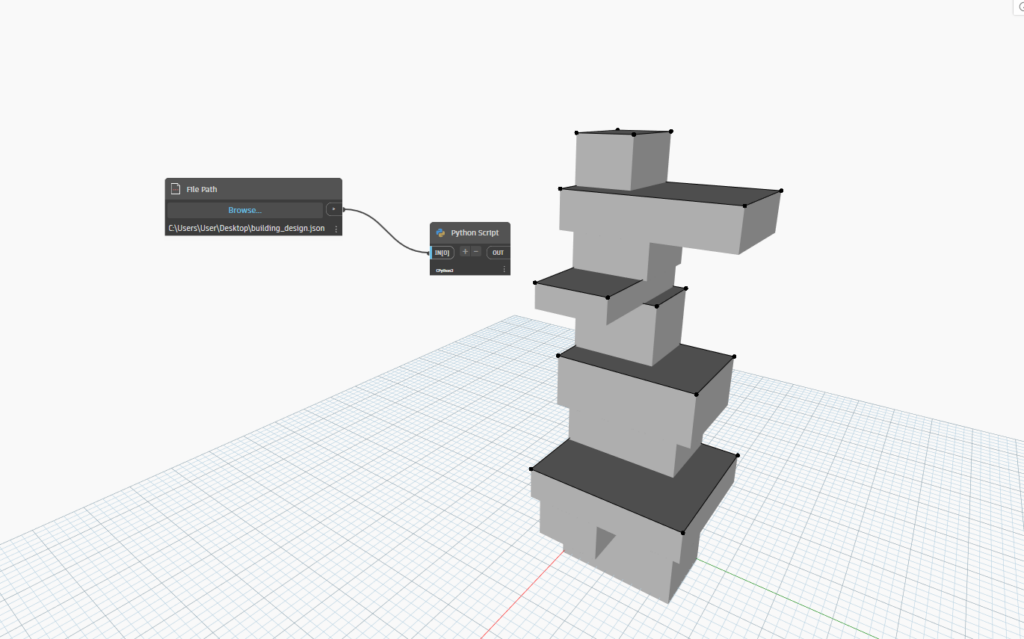
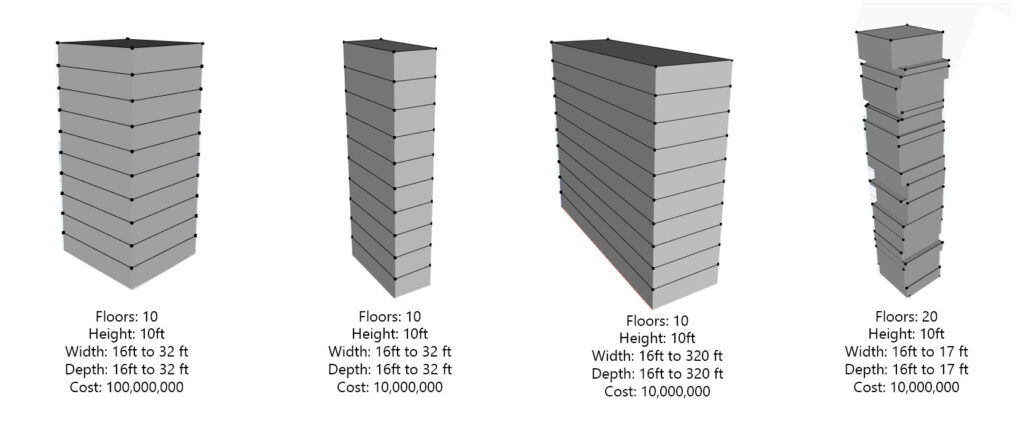
Adjusting the Algorithm
If you check the preview image in Dynamo you will see that the shape is a little bit weird (we could set constrains for example floors cannot be larger than X and smaller that Y to limite the size, uniformity of the shape of the building, cost, etc).
In the end, it’s up to the user to define the limits based on the needs of the current project.
Future Potential and Next Steps in AEC Optimization
In this post, we demonstrated how to use GeneticSharp to solve a building design optimization problem in the AEC, but the power of this is gigantic.
It could be attached, for example, to a LLM and you could make requirements on natural language on how you want your building to look, check against construction codes, generate efficient layouts, etc.
Stay tuned for more advanced examples and insights on leveraging genetic algorithms in AEC software development.
If you want to access the project where we develop this code, you can check out the Github Repo.
Valentin Noves
I'm a versatile leader with broad exposure to projects and procedures and an in-depth understanding of technology services/product development. I have a tremendous passion for working in teams driven to provide remarkable software development services that disrupt the status quo. I am a creative problem solver who is equally comfortable rolling up my sleeves or leading teams with a make-it-happen attitude.
