3D Matrix Transformations in C#: a Beginners Guide

For those using software such as Rhino or Revit, it’s evident that adjusting 3D geometry is far from easy. You need to understand how Euclidean space works, clockwise, and counterclockwise axis, and how the software expects you to handle it.
However, after resolving an issue in one software, you often need to start over in another due to differences in how they handle transformations.
The beginning. What is a 3D transformation?
For those of you who are not familiar with transformations, let me walk through an example.
Let’s say moving an object from one point to another.
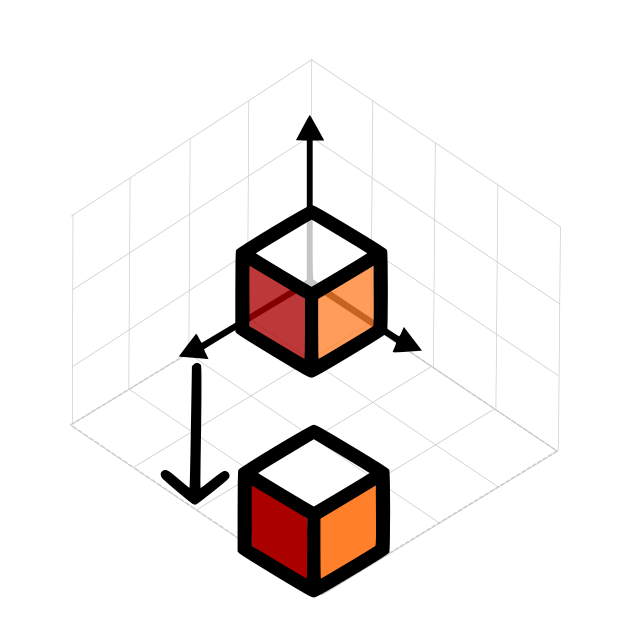
cube.Position.X += 4;
cube.Position.Y += 4;
Easy, don’t you think? We moved the object from its current location to a new one (in this case added 4 units in X, 4 in Y, and 0 on Z).
Next step is to scale its height by two.
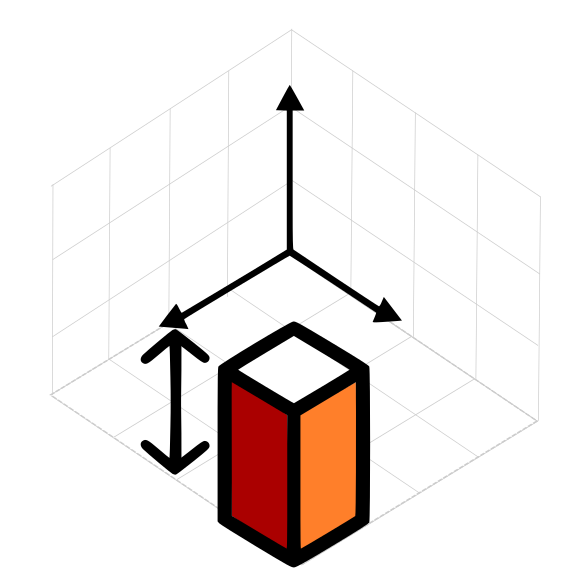
cube.Scale( new Vector(1,1,2));
We scaled the not-longer-a-cube geometry in Z by 2, leaving X and Y the same scale.
Now, rotate the object 90 degrees in a clockwise direction:
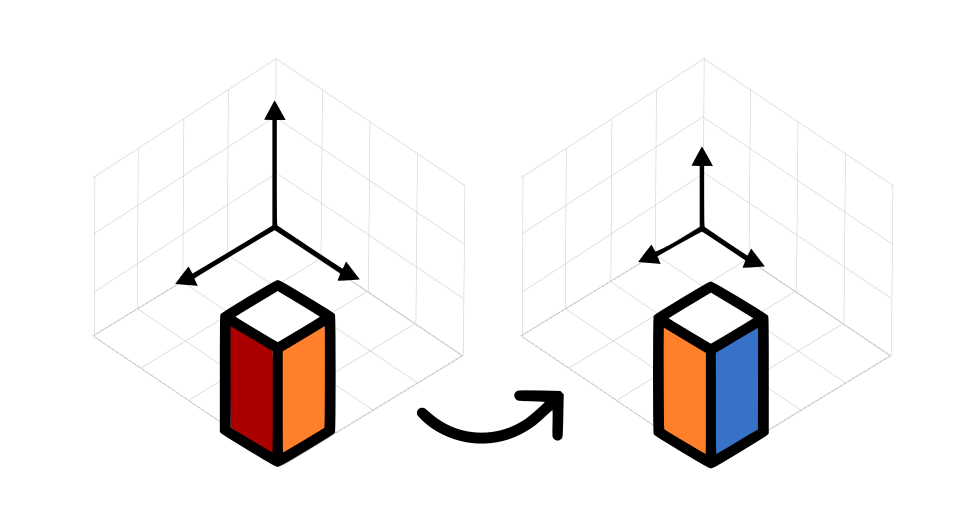
var pivot = new Point(3.5,3.5,0);
x.Rotate(pivot, 90);
This part needs an extra step. We not only need the angle we want to rotate but also the pivot point of the rotation itself. In this case the center of the XY plane.
Now imagine you have to do this transformation for your 1k elements in the model! Sure it’s easy with the pseudo-code I’m using but in real life you may not face the same interface.
This is where matrix transformations prove to be advantageous:
What is a Matrix?
A Matrix is a 2D array of numbers presented like below, in this case an identity matrix. I has no transformation.
One matrix can encode the translation, orientation, scale, and shearing of an object in 3D.
How does a Matrix work?
Below you can see an identity matrix (no transformation), a translation matrix and a scale matrix.

Note how the transformations for each axis are inputted. The translation has tx, ty, and tz meaning a point X, Y, Z, and the scale has a value for each axis to be scaled (sx, sy, sz).
Below you will find the rotation matrices for rotations on X, Y and Z axis, where d are the degrees of rotation

With all this information, if we want to do the same transformation we did before, we just need to apply one matrix
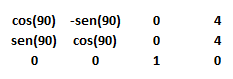
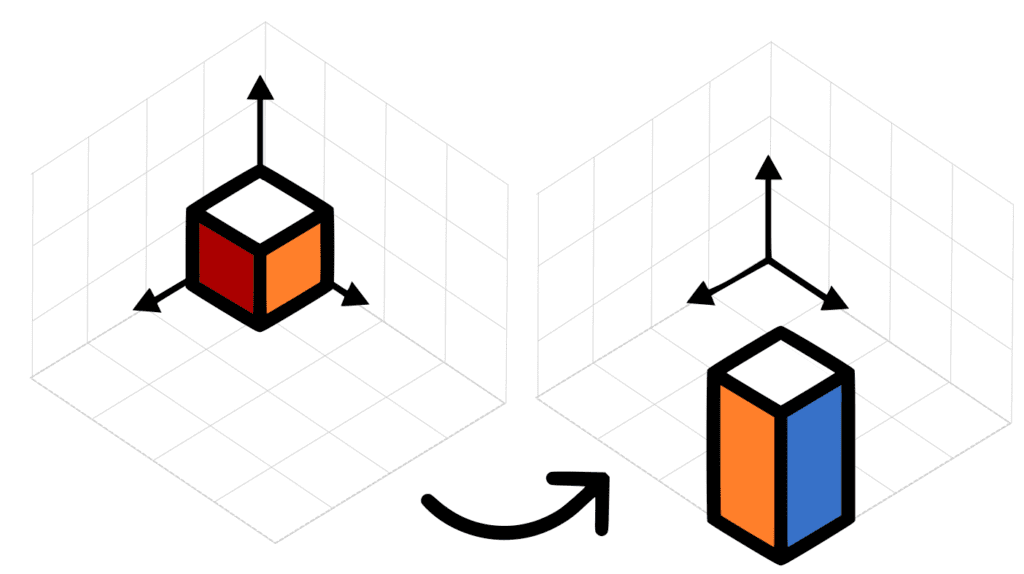
Matrix Calculations with 3D Software
When you’re short on time to grasp all these concepts, consider using System.Numerics for assistance!
Most 3D software expose an API to their transformation matrices. But this means that you need to create logic for each software to achieve the same results.
Revit and Navisworks provide a few classes that handle the most common operations such as invert, add, subtract, multiply, etc. But, of course, they don’t expose the same methods and need custom implementations to achieve the same results.
What we propose you is to wrap all the transformation logic with something like a repository pattern.
You create the connections and leave this library to handle all the calculations for you and expose all information you need.
Here there are a few samples of how we use the agnostic library System.Numerics to do matrix calculations.
How to do Matrix Calculations using the agnostic library System.Numerics?
The following code sample shows how to change a points Z up axis to Y up.
public static float[] ZToY(this float[] point)
{
var trans = new Matrix4x4();
trans.Translation = new Vector3((float)point[0], (float)point[1], (float)point[2]);
var finalMatrix = Matrix4x4.Multiply(Matrix4x4.Multiply(_rotationMatrix, trans),
_invertedRotation);
var translation = finalMatrix.Translation;
return new float[] { translation.X, translation.Y, translation.Z };
}
The same principle but translating the whole matrix in this case, we start from a Navisworks transformation class.
public static float[] ZToYTransform(this InwLTransform3f3 transform)
{
//Important casting to be made before quering the information from the COM class
dynamic matrix = transform.Matrix;
var _m = (Array)(object)matrix;
//Recreate current matrix
var _matrix = new Matrix4x4(
(float)(double)_m.GetValue(1), (float)(double)_m.GetValue(2), (float)(double)_m.GetValue(3), 0f,
(float)(double)_m.GetValue(5), (float)(double)_m.GetValue(6), (float)(double)_m.GetValue(7), 0f,
(float)(double)_m.GetValue(9), (float)(double)_m.GetValue(10), (float)(double)_m.GetValue(11), 0f,
(float)(double)_m.GetValue(13), (float)(double)_m.GetValue(14), (float)(double)_m.GetValue(15), 1f);
//Rotate, and translate and rotate back
var finalMatrix = Matrix4x4.Multiply(Matrix4x4.Multiply(_rotationMatrix, _matrix),
_invertedRotation);
//Rotate, and translate and rotate back
return finalMatrix.MatrixFromTransformation();
}
⚠️ Note: Revit has it’s X axis on the opposite side than other 3D software. Remember to place a minus in front of the angle when creating the rotation matrix
Conclusions
You can see that after accessing the information from the specific software classes, using the library Numerics. We standardize the steps to do the calculations. It’s a great option to start your Geometry library and deploy it on all your BIM projects.
Do you have a different process for dealing with Matrices?
Must go references
If matrices is something you want to delve deeper into, we really recommend the series of videos from 3Blue1Brown talking about linear transformations.
Pablo Derendinger
https://www.e-verse.comI'm an Architect who decided to make his life easier by coding. Curious by nature, I approach challenges armed with lateral thinking and a few humble programming skills. Love to work with passioned people and push the boundaries of the industry. Bring me your problems/Impossible is possible, but it takes more time.
